あんちっく無料ゲーム

祝『けろりんむら(通信対戦)』公開の件♪(＾＾)
「あんちっく無料ゲーム♪」の
[新型将棋通信対局]ページに
『けろりんむら(通信対戦)』(たね企画室様考案)が
公開されました♪(＾＾)
　↓
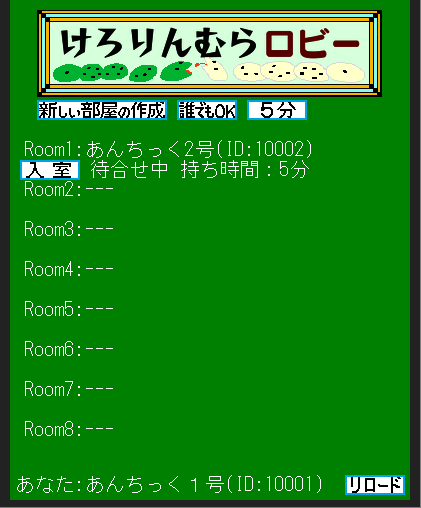
●『けろりんむら』とは？

めだまがえる達の陣地突入ゲームです♪
駒は八方向に１マス進め、
１つ目の少ない駒を取れます。(１は５を取れます♪)
先に自分の駒が相手の陣地に３つゴールすれば勝ち♪
※ゴールした駒は取られません！動けません！
※お互いの駒が２つ以下になると引き分け判定！
詳細ルール(たね企画室様考案)

●実際の画像♪
　※スマホでも遊べますが、
　　１秒以内に通信完了できないとバグるので、
　　真剣勝負には向かないかもです♪
　　(交流戦などには使えます♪)

『本将棋(通信対戦)』
『始点ワープ将棋(通信対戦)』
『めだまがえる(通信対戦)』
のロビーでの通信を強化しました～♪＼(＾＾)／
(元々、そこそこ安定してましたが♪)

具体的には、
通信不良でサーバー上に
データ欠損などの異常データが一時的に書き込まれた場合に、
それを正規データと扱わないように、
末尾部分の数字でチェックするようにしました♪
(「チェックディジット」と呼びます♪)

これまで「チェックディジット」による通信強化は、
●ＩＤ管理
●対局中のデータ
を対象としてきましたが、
今回のver260で
●ロビーのデータ
も対象としました♪＼(＾＾)／

■未解決事項
「通信エラー」直後に
ロビーの表示が乱れる時があるみたいです。
●Ａさんの募集が２～３個に分身する
●募集の位置がズレる
など
ちなみに表示だけが一時的におかしくなるだけなので、
ご安心ください♪
「おかしいな？」と感じたら[リロード]ボタンを押してください♪
ｍ(＾＾；)ｍ

『第４回新将棋まつり』ネット上開催！＼(＾ワ＾)／
名古屋、京都で開催した『新将棋まつり』ですが、
今回はネット上開催いたします♪
『第４回新将棋まつり』の詳細情報はこちら！！
■主催者：あんちっく
■主なイベント：ポイントレース大会
全て２１～２４時開催！各大会先着８名！
・７月１６日(金)：『京将棋』大会<将棋ったーβ>
・７月１８日(日)：『シュラハ』大会<ユドナリウム>
・７月２３日(金)：『中将棋』大会<ＳＤＩＮの中将棋>
・７月２４日(土)：『めだまがえる』大会<あんちっく無料ゲーム♪>
・７月２５日(日)：『四人将棋』大会<ＳＤＩＮの四人将棋>
■参加資格：
ツイッターアカウント(連絡手段であるため)
パソコンでの対局推奨
■参加方法：
あんちっくツイッター(@antic_akira)に連絡を♪
エントリー状況やポイント状況はこちらで分かります♪
　第４回新将棋まつりのポイントレース成績
■総合優勝賞品
・表彰状(手作り)
・『集大成将棋2019』【第１～４弾】※
・『カード将棋』
・『京将棋ペンタスロンセット』※
・『正体隠匿将棋(雪中将棋)』※
・『神威将棋』
(※は売り切れていない場合に限る)
レターパックでお送りいたします♪
■最後に：
ネット対局という事で分からない事も多いと思いますが、
　運営側が全力でサポートしますので、
　気軽に参加してみてください♪＼(＾＾)／

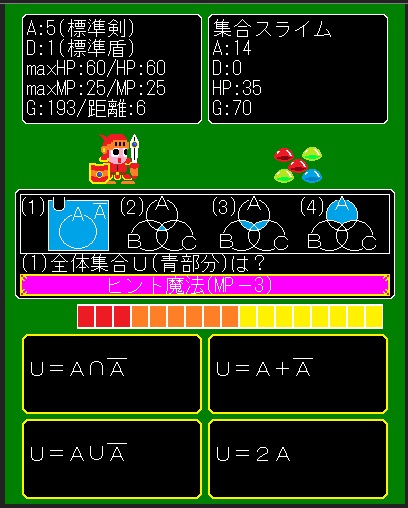
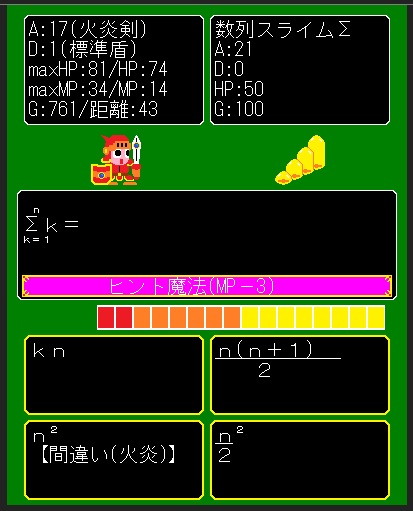
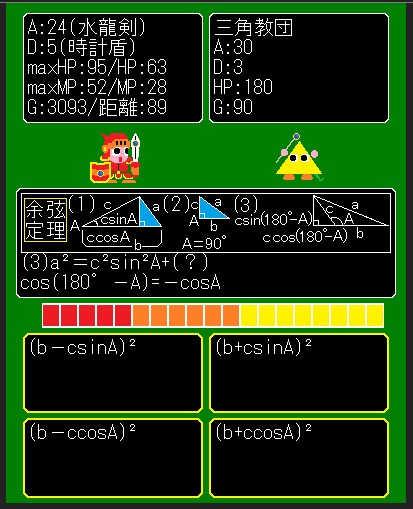
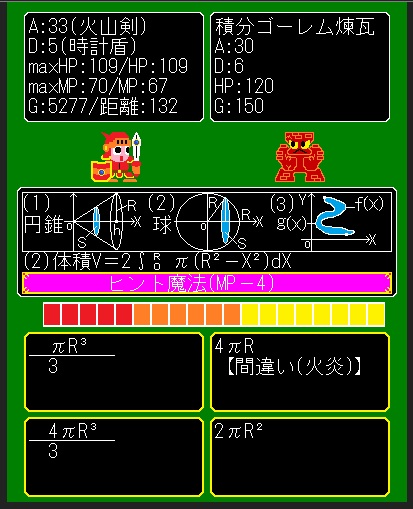
祝『数学魔法剣士(高校レベル)』完成♪＼(＾ワ＾)／
『数学魔法剣士(高校レベル)』ようやく完成しました！＼(＾ワ＾；)／
あんちっく無料ゲーム♪サイトの[無料ブラウザゲーム]で公開中です♪

●素早く解答すると2倍、3倍の攻撃力！
●ヒント魔法をガンガン使おう！
●オートセーブ方式♪　プレイ時間：約９０分
(ゲーム終了は画面を閉じればＯＫ！オートセーブされてます♪)
●数Ⅰ、数Ⅱ、数Ⅲ、数Ａ、数Ｂ、数Ｃ♪(高校レベル)【注：高難易度】
●補足→A:攻撃力－D:防御力=ダメージ♪
●復習に最適！
●フォント問題：MSゴシックで表示しています♪
　iPhoneなどはMSゴシックがないので、文字がズレると思いますので、
　タイトル画面の[文字上][文字下]ボタンで
　2/3の表示が正しくなるよう微調整してみてください♪
●たまにBGMが1曲演奏終了するまで止まらなくなりますが、
　それほど深刻な内容ではないので、ご了承を～！
●特殊効果を持つ剣盾が増加！！

ちなみに中学校レベルの続編なんですが、
中学校レベルの開発期間：１８日間
高校レベルの開発期間：半年(１８０日間)
と、１０倍近い開発期間がかかりました…。orz
(単純に高校の方が中学よりも学習範囲が広いんですね…。)

なお、
「高等学校学習指導要領（平成３０年告示）」準拠です♪
２０１９年～２０２２年は学習内容の過渡期であり、
２０２２年に新版になるのですが、
学習内容そのものは順番を入れ替えただけで
大きな違いはありません♪(＾＾)
『数学魔法剣士』としては、
モンスターの登場に合わせた
オリジナルの出題順となっており、
あまり気にせず遊ぶ事ができると思います♪ｄ(＾皿＾)ｂ

祝『めだまがえる(通信対戦)』公開の件♪(＾＾)
「あんちっく無料ゲーム♪」の
[新型将棋通信対局]ページに
『めだまがえる(通信対戦)』(たね企画室様考案)が
公開されました♪(＾＾)
　↓
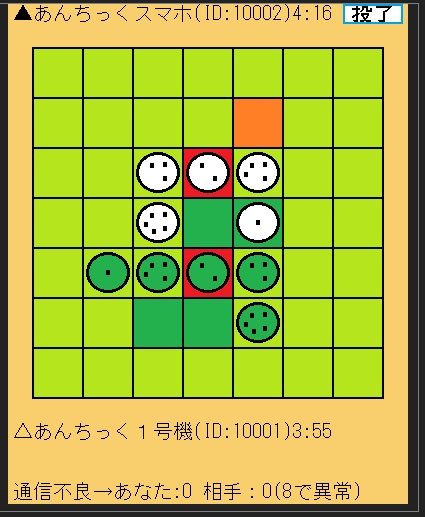
●『めだまがえる』とは？

めだまがえる達の追いかけっこゲームです♪
駒は八方向に１マス進め、
１つ目の少ない駒を取れます。(１は５を取れます♪)
駒を取るとひっくり返るか選択ができます。
駒の裏側は赤目で１つ目が多いです。(５の裏は1)
先に相手の駒を３つ取れば勝ち♪
詳細ルール(たね企画室様考案)
※ブラウザゲーム版では、
　お互いに駒を２つずつ取るとゲーム終了し、
　相手の駒を取れる駒数が多い方の判定勝ちです♪

●実際の画像♪
　※スマホでも遊べますが、
　　１秒以内に通信完了できないとバグるので、
　　真剣勝負には向かないかもです♪
　　(交流戦などには使えます♪)

『本将棋(通信対戦)』
『始点ワープ将棋(通信対戦)』
の終局図ですが、
対局後も確認できるように改善しました♪(ver250)
(今までは、勝敗表示がポップアップであり、
終局図の一部を隠してました…。)

また、
HTML4.01→HTML5にしました♪(ver250)
ｄ(＾＾)

なお、
新型将棋の新作が追加される予定です♪(＾＾)

『本将棋(通信対戦)』
『始点ワープ将棋(通信対戦)』
の対局中の通信を強化しました～♪＼(＾＾)／
(元々、そこそこ安定してましたが♪)

対局中の通信データの末尾が
片方のプレイヤーのＩＤ番号なんですが、
ＩＤ５桁化に伴い、
「末尾部分が５桁じゃなきゃ異常データ」
としてブロックする仕様にしました～♪ｖ(＾＾)

【背景】
異常通信時のサーバー上テキストファイル
に対する書込ミスに対しては、
書込ミスを検知して再書込するのですが、
再書込までの１秒の間に、
相手側が異常データを読込してしまう問題が
見つかりました。(発生頻度：低)
「異常データを書き込まない」が
理想的でしたがプログラム上難しく、
次善策である
「異常データを読み込まない」で
対策しました♪＼(＾＾；)
(これで、かなり通信強化されたはずです♪)

『本将棋(通信対戦)』
『始点ワープ将棋(通信対戦)』
ですが、
新規発行ＩＤが０にリセットされてしまう問題があり、
本日よりＩＤ５桁にするなどして、
対策を行いました♪
(＾＾)

【詳細】
ＩＤ４桁以下の方には
ログイン時に
ＩＤ５桁が新規発行されます♪

【どんな問題だったの？】
サーバー側に
ＩＤを管理するテキストファイルが
あるのですが、
通信失敗時に０が上書きされていました。
ＩＤ５桁でない上書きを停止させたり、
通信時にＩＤが５桁かどうか
調べる事で、通信失敗を
判断できるようにしました♪
かなりの強化なので、ほぼ解決かと♪
(＾＾；)

『数学魔法剣士(中学校レベル)』攻略法！ｄ(＾ワ＾)ｂ

【１】近似値、真の値、誤差とは？

やや分かりにくいと感じたので補足します♪(＾＾)

「真の値」：本当の値
（例：１７．１４１４２１３５６１７３２０５０８…）
「近似値」：端数を省略し分かりやすい数字にした値
（例：１７）
「誤差」：｜近似値ー真の値｜
（例：０．１４１４２１３５６１７３２０５０８…）

「近似値」は、そもそも分かりやすくした値の事ですが、
例えば商品の設計図のように
計算によって求められた理想とする値や、
とりあえず決めた基準となる値も、
実際の「真の値」(加工精度の都合上バラつく)に対して、
ぴったりの値になるので、「近似値」と呼ばれます♪＼(＾＾；)
この意味の「近似値」(理想とする値、基準となる値)からの
「真の値」のズレが「誤差」です♪(＾＾)

【２】２の８乗、２の１０乗！

２の８乗は、２を８回かけたもの
２Ｘ２Ｘ２Ｘ２Ｘ２Ｘ２Ｘ２Ｘ２＝２５６
２の１０乗は、２を１０回かけたもの
２Ｘ２Ｘ２Ｘ２Ｘ２Ｘ２Ｘ２Ｘ２Ｘ２Ｘ２＝１０２４
です♪(＾＾；)
「こんなの分からないし、何の役に立つのか？」と
思われるかもしれませんが、
コンピューターの世界(ＯＮ／ＯＦＦの２進法の世界)では
頻出の計算なので、暗記しても良い内容となります♪(＾＾)

【３】たすき掛け(因数分解)

中学校ではなく高校で習うケースもあるみたいなんですが、
覚えておくと便利です♪ｄ(＾＾)
(ちなみに、「たすき」は斜めに着用するヒモや布で
ここでは、「斜め」の意味で使われています♪)
まず、
６Ｘ²－５Ｘ－４＝(ＡＸ＋Ｂ)(ＣＸ＋Ｄ)とします♪
ここで、
・Ｘ²の係数に注目すると、
ＡとＣにはＡ×Ｃ＝６になる組み合わせが入る。
・Ｘの無い数字部分に注目すると、
ＢとＤにはＢ×Ｄ＝－４になる組み合わせが入る。
と分かります♪
さらに、
・Ｘの係数に注目すると、
Ａ×Ｄ＋Ｂ×Ｃ＝－５になる組み合わせが入る。
と分かります♪
パズルみたいなものなんですが、
これを解く時に便利な書き方が
以下のように二段にして書く方法です♪
ＡＸ　　＋Ｂ
ＣＸ　　＋Ｄ
ちなみにＡ×Ｄ＋Ｂ×Ｃ＝－５となる
組み合わせを見つけるのが大変なんですが、
この書き方だと、
斜めどうしを掛け算するので…
「たすき掛け」と呼びます♪(＾Ｕ＾)
(なお、パズルみたいなもので、
難易度が高いものも出題されます！ご了承を♪)

なお、Ｘ²の係数が１の場合は、
「たすき掛け」はかなり簡単になります♪
Ｘ²＋５Ｘ＋６＝(ＡＸ＋Ｂ)(ＣＸ＋Ｄ)とすると、
Ａ＝１、Ｃ＝１と分かってしまいます♪
二段に書くと
Ｘ　　＋Ｂ
Ｘ　　＋Ｄ
です♪
・Ｘの無い数字部分に注目すると、
ＢとＤにはＢ×Ｄ＝６になる組み合わせが入る。
・Ｘの係数に注目すると、
１×Ｄ＋Ｂ×１＝Ｂ＋Ｄ＝５になる組み合わせが入る。
となります♪

【４】連立方程式、２次方程式が難しい！？

はっきり言って強敵です！
ヒント魔法使用を前提として戦いましょう♪(＾＾)
なお、紙とペンを使用してもＯＫです♪
(＾＾；)＜スマホ対応ゲームとは…。

【５】正多面体とは？

ドット絵で正多面体の絵を描くのは難しく、
文章問題だったので分かりにくいと思います…(＾＾；)＞
こちらのWikipediaのページに
正多面体の画像がありますので、ご参照ください♪
「プラトンの立体」とも呼ぶみたいです♪(＾＾)

【６】相似を使う面積問題

図形問題は難問なので、いくつか解説しようと思います♪(＾＾；)

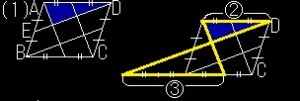
(１)青色の面積は、四角形ＡＢＣＤの何倍か？
まず、ＡＢ＝ＣＤ，ＡＤ＝ＢＣより
四角形ＡＢＣＤは平行四辺形と分かります♪
次にＥＤ，ＢＣを延長すると、(１)の右図のようになり
３：２の比を持つ相似の三角形が現れます。
(図では、分かりやすいように③、②と書いています♪)
すると平行四辺形の高さと、
青色の三角形の高さの比は５：２と分かり、
２／５倍の高さと分かります。

平行四辺形ＡＢＣＤの底辺をＬ、高さをｈとすると、
平行四辺形ＡＢＣＤの面積＝底辺×高さ＝Ｌｈ
青色の三角形の面積＝底辺×高さ÷２＝Ｌ×２／５ｈ÷２＝１／５Ｌｈ
と分かり、１／５倍の面積と分かります♪
(注：今回の解説では分数を／で表現しています。(＾＾；))

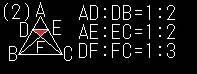
(２)△ＤＥＦは△ＡＢＣの何倍の面積？
まず、△ＡＤＥと△ＡＢＣは
ＡＤ：ＡＢ＝１：３、ＡＥ：ＡＣ＝１：３、∠Ａ＝∠Ａより
「２組の辺の比とその間の角が、それぞれ等しい」
と言えるので、１：３の比を持つ相似の関係です♪
これによりＤＥとＢＣが平行というのも分かります♪
すると△ＤＥＦと△ＣＢＦも
「２組の角が、それぞれ等しいとき」
と言えるので、１：３の比を持つ相似の関係です♪

△ＡＢＣの底辺をＬ、高さをｈとすると、
△ＤＥＦの底辺は１／３Ｌ、
△ＤＥＦの高さは、
ＢＣからＤＥまでの高さが
△ＡＤＥと△ＡＢＣの相似比＝１：３よりｈ×２／３で、
さらに△ＤＥＦと△ＣＢＦの相似比＝１：３より
ｈ×２／３×１／４＝１／６ｈと分かります♪

△ＡＢＣの面積＝底辺×高さ÷２＝Ｌｈ÷２
△ＤＥＦの面積＝底辺×高さ÷２
＝１／３Ｌ×１／６ｈ÷２＝１／１８Ｌｈ÷２
と分かり、１／１８倍の面積と分かります♪

なお、文字で解説すると、長めになりますが…
・平行な辺を持つ三角形
・辺の比が等しい三角形
などが登場したら、相似の可能性を疑いましょう♪＼(＾＾；)
そして、相似と分かったら、
相似の比で長さの比率が分かり、
そこから面積の比率も分かります♪ｄ(＾皿＾)

【７】三角形の合同条件の問題について

三角形の合同条件の証明の問題では、
合同を証明するため等しい３ヶ所を答えてください♪
ただし、問題文の最後に(　)があり、
１ヶ所がすでに表示されている場合は、
残りの２ヶ所を答えるだけでＯＫです♪(＾＾)
(図形問題は、中学校レベルの最難関ポイントです♪
制限時間に焦りますが…、しっかり正解しましょう♪)
↓
2020/7/31追記：ver1.01修正点
証明問題の選択肢を作り直しました♪＼(＾＾；)
間違いの選択肢の中に
「中学の知識では解けないので不正解」
「最短手順での証明ではないので不正解」
というのを
混ぜていたんですが、
知識量の多い人や頭の回転の速い人にとっては、
「正解が複数あるように見える！」
という問題を引き起こしていたようなので、
上手く修正しました♪(＾＾；)

【８】交点はなぜ連立方程式で求まるの？

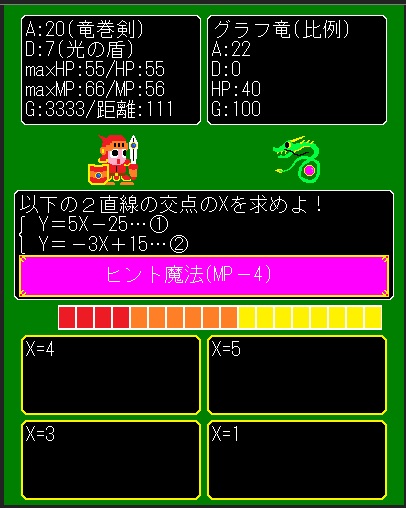
①②はそれぞれの直線上にある
点(Ｘ，Ｙ)の組み合わせ全てを表現しています♪
①②の直線上に同時に存在するのが交点なので、
①②を別々ではなく、連立方程式として解くと、
交点(Ｘ，Ｙ)が求まります♪

【９】ダークキングが強い！

たまにオリジナルの超難問を繰り出してきて、
ヒント魔法を使っても、
計算が難しい場合があります♪(＾＾；)
暗算が難しい場合は、
紙とペンを使用してもＯＫです♪ｄ(＾ワ＾；)

【１０】お店の品ぞろえが毎回異なる！
小学校レベルと違い中学校レベルでは、
お店に登場する剣盾に乱数を使用しています♪
性能を見極めて購入すると良いです♪
なお、中学校レベルの方が、
ややお金に余裕ができるので、
色々と買物も楽しめます♪ｄ(＾Ｕ＾)

それでは、
クリアまで頑張ってみてください♪＼(＾ワ＾)／

『数学魔法剣士(小学校レベル)』攻略法！ｄ(＾皿＾)ｂ

【１】「３桁の割り算」のヒント魔法

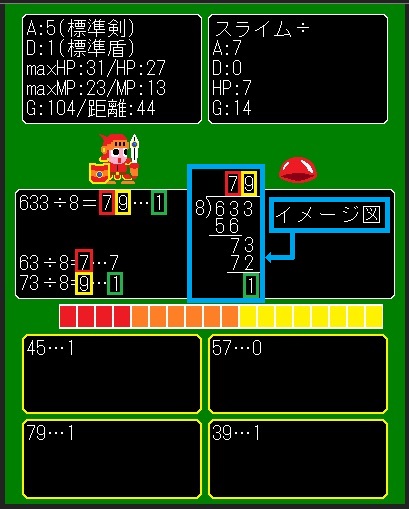
イメージ図を書くと、こんな感じです♪
上の桁から順番に計算しています♪
ちょっと分かりにくいヒント魔法ですね…(＾ワ＾；)>

【２】秒速を時速に変換する問題

問題：１０[m/秒]の風は何[km/時]？
ヒント魔法：１[時間]＝３６００[秒]、１[km]＝１０００[m]

秒速を時速に変換する方法ですが、
１[秒]で１０[ｍ]進むならば、
１[時間]つまり３６００[秒]では３６００倍進みます♪
つまり１０[ｍ]Ｘ３６００＝３６０００[ｍ]進みます。
これを[ｋｍ]に変換するには、
１[km]＝１０００[m]なので、
１０００で割ればＯＫです♪
３６０００÷１０００＝３６[km]
つまり１[時間]で３６[km]進むので
３６[km/時]となります♪
このように１[時間]進んだ場合で考えます♪(＾＾)
ちなみに１０[m/秒]＝３６[km/時]は、
何となく覚えておくと便利かもです♪ｄ(＾＾)

【３】追いかけ問題

問題：
２８０m先を７[m/秒]で進む車Aを３５[m/秒]で車Bが追いかけると
何[m]進んだ所で追いつく？

車Ｂは１[秒]で３５[ｍ]
車Ａは１[秒]で７[ｍ]進むので
1[秒]で２８[ｍ]追いつきます。
このため、２８０÷２８＝１０より
１０[秒]で追いつくのですが、
それまでに進んだ距離は、
車Ｂで考えれば
３５[m/秒]Ｘ１０[秒]＝３５０[ｍ]となります♪
車Ａで考えるならば
２８０[ｍ]＋７[m/秒]Ｘ１０[秒]＝３５０[ｍ]ですね♪(＾＾)

【４】「平均の速度」問題【難問】

問題：
２地点を、行きは７[km/時]、帰りは１３[km/時]で進む時
往復の平均の速度は何[km/時]？

まず、「平均の速度」ですが、
(７＋１３)÷２＝１０で１０[km/時]ではありません。
７[km/時]、１３[km/時]で進んだ時間が同じなら
この計算式で正しいのですが、
同じ距離を、行きと帰りで違う速度で進むので、
行きと帰りの時間が違うというのがポイントです。

今回は２つの解き方を紹介しようと思います♪(＾＾)

【解き方１】２地底の距離を決めてしまう！
例えば、２地点の距離を
７Ｘ１３＝９１[ｋｍ]とすると、
行き：９１[km]÷７[km/時]＝１３[時間]
帰り：９１[km]÷１３[km/時]＝７[時間]
となります♪
往復９１[km]Ｘ２＝１８２[km]の距離を２０[時間]で進んだので、
「平均の速度」は、
１８２[km]÷２０[時間]＝９．１[km/時]となります♪

ちなみに、２地点の距離が問題文にないので、
困ってしまうかもですが、
計算しやすい距離を想定して解いてＯＫです♪
これは、例えば１０倍の９１０[km]を想定した場合、
かかる時間も１０倍の２００[時間]となり、
１８２０[km]÷２００[時間]＝９．１[km/時]
となるように、距離と時間がともに１０倍されても、
速度は変わらないという性質があるからです♪(＾＾)
(ただ、２地点の距離がどうであれ、
答えの「平均の速度」には影響しないというのは
分かりにくい内容でもあるので、
今回は【解き方２】も用意しました♪)

【解き方２】２地点の距離□[km]とする。
虫食い算の□を使う方法です♪
２地点の距離□[km]とすると…
行き：□[km]÷７[km/時]＝□÷７[時間]
帰り：□[km]÷１３[km/時]＝□÷１３[時間]
となります♪
往復２Ｘ□[km]の距離を、
行きと帰りにかかった時間の合計で進んだので、
計算式としては、

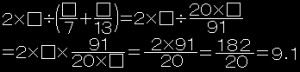
となり、
「平均の速度」は９．１[km/時]と分かります♪
(□は同じ数字なので消えます♪)
(分数の計算になるので大変ですが…)

それにしても、こんな難しい問題が
小学校で出題されているとは
知りませんでした…(＾＾；)
なお、小学生の方は、現在解けなくても
心配しなくてＯＫです♪
中学生で習うＸ(エックス)を習得すれば、
【解き方２】みたいな方法で、
簡単に解けるようになります♪
ｄ(＾皿＾)＜『数学魔法剣士(中学校レベル)』もよろしく～♪