【1】「3桁の割り算」のヒント魔法
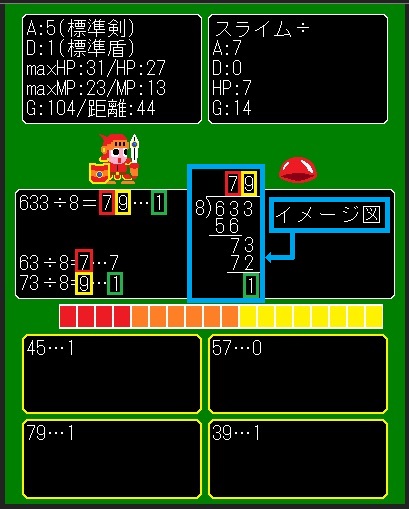
イメージ図を書くと、こんな感じです♪
上の桁から順番に計算しています♪
ちょっと分かりにくいヒント魔法ですね…(^ワ^;)>
【2】秒速を時速に変換する問題

問題:10[m/秒]の風は何[km/時]?
ヒント魔法:1[時間]=3600[秒]、1[km]=1000[m]
秒速を時速に変換する方法ですが、
1[秒]で10[m]進むならば、
1[時間]つまり3600[秒]では3600倍進みます♪
つまり10[m]X3600=36000[m]進みます。
これを[km]に変換するには、
1[km]=1000[m]なので、
1000で割ればOKです♪
36000÷1000=36[km]
つまり1[時間]で36[km]進むので
36[km/時]となります♪
このように1[時間]進んだ場合で考えます♪(^^)
ちなみに10[m/秒]=36[km/時]は、
何となく覚えておくと便利かもです♪d(^^)
【3】追いかけ問題

問題:
280m先を7[m/秒]で進む車Aを35[m/秒]で車Bが追いかけると
何[m]進んだ所で追いつく?
車Bは1[秒]で35[m]
車Aは1[秒]で7[m]進むので
1[秒]で28[m]追いつきます。
このため、280÷28=10より
10[秒]で追いつくのですが、
それまでに進んだ距離は、
車Bで考えれば
35[m/秒]X10[秒]=350[m]となります♪
車Aで考えるならば
280[m]+7[m/秒]X10[秒]=350[m]ですね♪(^^)
【4】「平均の速度」問題【難問】

問題:
2地点を、行きは7[km/時]、帰りは13[km/時]で進む時
往復の平均の速度は何[km/時]?
まず、「平均の速度」ですが、
(7+13)÷2=10で10[km/時]ではありません。
7[km/時]、13[km/時]で進んだ時間が同じなら
この計算式で正しいのですが、
同じ距離を、行きと帰りで違う速度で進むので、
行きと帰りの時間が違うというのがポイントです。
今回は2つの解き方を紹介しようと思います♪(^^)
【解き方1】2地底の距離を決めてしまう!
例えば、2地点の距離を
7X13=91[km]とすると、
行き:91[km]÷7[km/時]=13[時間]
帰り:91[km]÷13[km/時]=7[時間]
となります♪
往復91[km]X2=182[km]の距離を20[時間]で進んだので、
「平均の速度」は、
182[km]÷20[時間]=9.1[km/時]となります♪
ちなみに、2地点の距離が問題文にないので、
困ってしまうかもですが、
計算しやすい距離を想定して解いてOKです♪
これは、例えば10倍の910[km]を想定した場合、
かかる時間も10倍の200[時間]となり、
1820[km]÷200[時間]=9.1[km/時]
となるように、距離と時間がともに10倍されても、
速度は変わらないという性質があるからです♪(^^)
(ただ、2地点の距離がどうであれ、
答えの「平均の速度」には影響しないというのは
分かりにくい内容でもあるので、
今回は【解き方2】も用意しました♪)
【解き方2】2地点の距離□[km]とする。
虫食い算の□を使う方法です♪
2地点の距離□[km]とすると…
行き:□[km]÷7[km/時]=□÷7[時間]
帰り:□[km]÷13[km/時]=□÷13[時間]
となります♪
往復2X□[km]の距離を、
行きと帰りにかかった時間の合計で進んだので、
計算式としては、
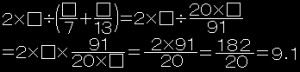
となり、
「平均の速度」は9.1[km/時]と分かります♪
(□は同じ数字なので消えます♪)
(分数の計算になるので大変ですが…)
それにしても、こんな難しい問題が
小学校で出題されているとは
知りませんでした…(^^;)
なお、小学生の方は、現在解けなくても
心配しなくてOKです♪
中学生で習うX(エックス)を習得すれば、
【解き方2】みたいな方法で、
簡単に解けるようになります♪
d(^皿^)<『数学魔法剣士(中学校レベル)』もよろしく~♪
