【1】近似値、真の値、誤差とは?

やや分かりにくいと感じたので補足します♪(^^)
「真の値」:本当の値
(例:17.14142135617320508…)
「近似値」:端数を省略し分かりやすい数字にした値
(例:17)
「誤差」:|近似値ー真の値|
(例:0.14142135617320508…)
「近似値」は、そもそも分かりやすくした値の事ですが、
例えば商品の設計図のように
計算によって求められた理想とする値や、
とりあえず決めた基準となる値も、
実際の「真の値」(加工精度の都合上バラつく)に対して、
ぴったりの値になるので、「近似値」と呼ばれます♪\(^^;)
この意味の「近似値」(理想とする値、基準となる値)からの
「真の値」のズレが「誤差」です♪(^^)
【2】2の8乗、2の10乗!

2の8乗は、2を8回かけたもの
2X2X2X2X2X2X2X2=256
2の10乗は、2を10回かけたもの
2X2X2X2X2X2X2X2X2X2=1024
です♪(^^;)
「こんなの分からないし、何の役に立つのか?」と
思われるかもしれませんが、
コンピューターの世界(ON/OFFの2進法の世界)では
頻出の計算なので、暗記しても良い内容となります♪(^^)
【3】たすき掛け(因数分解)

中学校ではなく高校で習うケースもあるみたいなんですが、
覚えておくと便利です♪d(^^)
(ちなみに、「たすき」は斜めに着用するヒモや布で
ここでは、「斜め」の意味で使われています♪)
まず、
6X²-5X-4=(AX+B)(CX+D)とします♪
ここで、
・X²の係数に注目すると、
AとCにはA×C=6になる組み合わせが入る。
・Xの無い数字部分に注目すると、
BとDにはB×D=-4になる組み合わせが入る。
と分かります♪
さらに、
・Xの係数に注目すると、
A×D+B×C=-5になる組み合わせが入る。
と分かります♪
パズルみたいなものなんですが、
これを解く時に便利な書き方が
以下のように二段にして書く方法です♪
AX +B
CX +D
ちなみにA×D+B×C=-5となる
組み合わせを見つけるのが大変なんですが、
この書き方だと、
斜めどうしを掛け算するので…
「たすき掛け」と呼びます♪(^U^)
(なお、パズルみたいなもので、
難易度が高いものも出題されます!ご了承を♪)

なお、X²の係数が1の場合は、
「たすき掛け」はかなり簡単になります♪
X²+5X+6=(AX+B)(CX+D)とすると、
A=1、C=1と分かってしまいます♪
二段に書くと
X +B
X +D
です♪
・Xの無い数字部分に注目すると、
BとDにはB×D=6になる組み合わせが入る。
・Xの係数に注目すると、
1×D+B×1=B+D=5になる組み合わせが入る。
となります♪
【4】連立方程式、2次方程式が難しい!?

はっきり言って強敵です!
ヒント魔法使用を前提として戦いましょう♪(^^)
なお、紙とペンを使用してもOKです♪
(^^;)<スマホ対応ゲームとは…。
【5】正多面体とは?
![]()
ドット絵で正多面体の絵を描くのは難しく、
文章問題だったので分かりにくいと思います…(^^;)>
こちらのWikipediaのページに
正多面体の画像がありますので、ご参照ください♪
「プラトンの立体」とも呼ぶみたいです♪(^^)
【6】相似を使う面積問題
![]()
図形問題は難問なので、いくつか解説しようと思います♪(^^;)
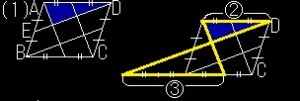
(1)青色の面積は、四角形ABCDの何倍か?
まず、AB=CD,AD=BCより
四角形ABCDは平行四辺形と分かります♪
次にED,BCを延長すると、(1)の右図のようになり
3:2の比を持つ相似の三角形が現れます。
(図では、分かりやすいように③、②と書いています♪)
すると平行四辺形の高さと、
青色の三角形の高さの比は5:2と分かり、
2/5倍の高さと分かります。
平行四辺形ABCDの底辺をL、高さをhとすると、
平行四辺形ABCDの面積=底辺×高さ=Lh
青色の三角形の面積=底辺×高さ÷2=L×2/5h÷2=1/5Lh
と分かり、1/5倍の面積と分かります♪
(注:今回の解説では分数を/で表現しています。(^^;))
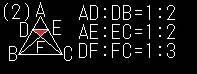
(2)△DEFは△ABCの何倍の面積?
まず、△ADEと△ABCは
AD:AB=1:3、AE:AC=1:3、∠A=∠Aより
「2組の辺の比とその間の角が、それぞれ等しい」
と言えるので、1:3の比を持つ相似の関係です♪
これによりDEとBCが平行というのも分かります♪
すると△DEFと△CBFも
「2組の角が、それぞれ等しいとき」
と言えるので、1:3の比を持つ相似の関係です♪
△ABCの底辺をL、高さをhとすると、
△DEFの底辺は1/3L、
△DEFの高さは、
BCからDEまでの高さが
△ADEと△ABCの相似比=1:3よりh×2/3で、
さらに△DEFと△CBFの相似比=1:3より
h×2/3×1/4=1/6hと分かります♪
△ABCの面積=底辺×高さ÷2=Lh÷2
△DEFの面積=底辺×高さ÷2
=1/3L×1/6h÷2=1/18Lh÷2
と分かり、1/18倍の面積と分かります♪
なお、文字で解説すると、長めになりますが…
・平行な辺を持つ三角形
・辺の比が等しい三角形
などが登場したら、相似の可能性を疑いましょう♪\(^^;)
そして、相似と分かったら、
相似の比で長さの比率が分かり、
そこから面積の比率も分かります♪d(^皿^)
【7】三角形の合同条件の問題について

三角形の合同条件の証明の問題では、
合同を証明するため等しい3ヶ所を答えてください♪
ただし、問題文の最後に( )があり、
1ヶ所がすでに表示されている場合は、
残りの2ヶ所を答えるだけでOKです♪(^^)
(図形問題は、中学校レベルの最難関ポイントです♪
制限時間に焦りますが…、しっかり正解しましょう♪)
↓
2020/7/31追記:ver1.01修正点
証明問題の選択肢を作り直しました♪\(^^;)
間違いの選択肢の中に
「中学の知識では解けないので不正解」
「最短手順での証明ではないので不正解」
というのを
混ぜていたんですが、
知識量の多い人や頭の回転の速い人にとっては、
「正解が複数あるように見える!」
という問題を引き起こしていたようなので、
上手く修正しました♪(^^;)
【8】交点はなぜ連立方程式で求まるの?
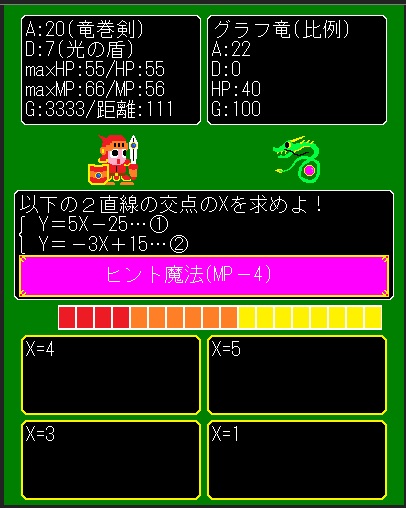
①②はそれぞれの直線上にある
点(X,Y)の組み合わせ全てを表現しています♪
①②の直線上に同時に存在するのが交点なので、
①②を別々ではなく、連立方程式として解くと、
交点(X,Y)が求まります♪
【9】ダークキングが強い!

たまにオリジナルの超難問を繰り出してきて、
ヒント魔法を使っても、
計算が難しい場合があります♪(^^;)
暗算が難しい場合は、
紙とペンを使用してもOKです♪d(^ワ^;)
【10】お店の品ぞろえが毎回異なる!
小学校レベルと違い中学校レベルでは、
お店に登場する剣盾に乱数を使用しています♪
性能を見極めて購入すると良いです♪
なお、中学校レベルの方が、
ややお金に余裕ができるので、
色々と買物も楽しめます♪d(^U^)
それでは、
クリアまで頑張ってみてください♪\(^ワ^)/
